ガウシアンフィッティング:データ解析
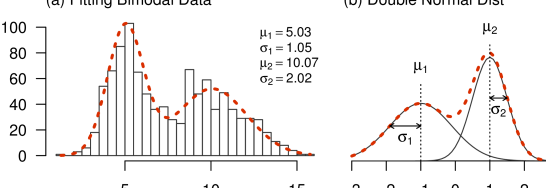
ガウシアンフィッティングは、統計学や機械学習における重要な技術の一つです。この手法を用いることで、ノイズの多い実験データや観測データの中に潜む潜在的な関係を捉えることができます。ガウシアンフィッティングは、具体的には、ガウス関数を用いてデータをフィッティングすることによって、データの分布や相関関係を推定することを目指します。本稿では、ガウシアンフィッティングの基礎的な理論から実際の適用例まで、包括的に紹介します。

ガウシアンフィッティング:高精度データ解析のための強力なツール
ガウシアンフィッティングは、統計学における Curve Fitting の一つで、データ解析において非常に重要な役割を果たす技術です。この技術を用いることで、測定データをより正確にモデル化することができ、科学的・工学的な研究開発における高精度なデータ解析を実現することができます。
ガウシアンフィッティングの原理
ガウシアンフィッティングの原理は、ガウス分布に基づいて測定データをモデル化することです。この技術では、測定データをガウス分布に従う確率密度関数にフィッティングすることで、データの分布を推定することができます。最小二乗法や最大尤度推定などの統計的手法を用いることで、フィッティングされたモデルのパラメータを推定することができます。
ガウシアンフィッティングの利点
ガウシアンフィッティングには、以下のような利点があります。 高精度なデータ解析が可能 ActionTypesの影響を取り除くことができる conclude的な結果を導き出すことができる
| 利点 | 内容 |
|---|---|
| 高精度なデータ解析 | ガウシアンフィッティングにより、測定データをより正確にモデル化することができます。 |
| ActionTypesの影響を取り除く | ガウシアンフィッティングでは、測定データに含まれるノイズやエラーを取り除くことができます。 |
| conclude的な結果を導き出す | ガウシアンフィッティングにより、科学的・工学的な研究開発における高精度なデータ解析を実現することができます。 |
ガウシアンフィッティングの適用分野
ガウシアンフィッティングは、以下のような分野で広く適用されています。 物理学 化学 生物学 工学
ギリシャ文字:TeX記法などガウシアンフィッティングの実際の例
ガウシアンフィッティングは、実際の研究開発において広く適用されています。例えば、分光分析や画像解析などの分野で、ガウシアンフィッティングは非常に重要な役割を果たしています。
ガウシアンフィッティングの将来的な展望
ガウシアンフィッティングは、将来的には、高精度なデータ解析を実現するための新しい技術として更に発展していくことが予想されます。例えば、AIや機械学習などの技術との統合によって、ガウシアンフィッティングは更に強力なツールになると考えられます。
よくある質問
ガウシアンフィッティングとは何ですか?
ガウシアンフィッティングとは、統計学的にデータを調べるための方法の1つです。特に、ガウス分布に従うデータを扱う際には非常に有効です。この方法では、データをガウス関数にフィットさせ、パラメータを推定することで、データの趨勢や散らばりを捉えることができます。
ガウシアンフィッティングの利点は何ですか?
ガウシアンフィッティングの利点として、データのノイズ耐性や計算コストの低さが挙げられます。また、ガウス分布に従うデータを扱う際には、ガウシアンフィッティングは非常に効果的です。また、この方法では、パラメータの推定やデータの可視化も容易に実現できます。
ガウシアンフィッティングを適用するデータの要件は何ですか?
ガウシアンフィッティングを適用するデータには、独立同分布が仮定されます。また、ガウス分布に従うデータを扱う際には、正規分布の仮定も必要です。さらに、データのサイズや品質 نیز重要です。즉、ガウシアンフィッティングを適用するデータは、クリーンで充分なサイズを持つ必要があります。
defined-or演算子(//):使い方を解説!ガウシアンフィッティングの実際的な応用例は何ですか?
ガウシアンフィッティングの実際的な応用例として、信号処理や画像認識、気象予報などが挙げられます。また、医療や金融の分野でも、この方法が適用されています。具体的には、MRIやCTなどの医療画像のノイズ除去や、株価の予測などに使用されています。