相関分析:相関係数行列&ヒートマップでデータ可視化!
データ分析において、相関分析は重要な手段です。データ間に隠れた関係を明らかにし、将来的に起こりうる現象を予測することができます。特に、複数の変数間の相関関係を把握することで、より的確な予測や意思決定を行うことができます。この記事では、相関係数行列やヒートマップを用いたデータ可視化の手法を紹介します。データの相関関係を可視化することで、より深く理解を深め、的確な意思決定を行うことができます。

データ可視化のツールとしての相関分析
相関分析は、統計学における分析手法の一つで、複数の変数間に存在する相関関係を捉えることを目的としています。この手法を用いることで、データの関係性を可視化し、より深く理解することができます。
相関係数行列とは
相関係数行列とは、複数の変数間に存在する相関関係を数値化したものを表しています。この行列には、各変数間に存在する相関係数が記載されており、係数の値が高ければ高いほど強い相関関係が存在していると言えます。相関係数は、-1から1の範囲で表され、0に近い値であるほど無相関状態にあると言えます。
| 変数A | 変数B | 変数C |
|---|---|---|
| 1.0 | 0.7 | -0.3 |
| 0.7 | 1.0 | 0.4 |
| -0.3 | 0.4 | 1.0 |
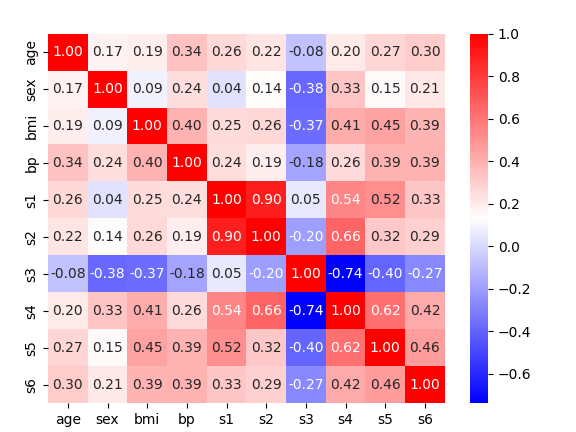
ヒートマップによる可視化
相関係数行列を基にして、ヒートマップを生成することで、データの関係性をよりわかりやすく可視化することができます。ヒートマップとは、色や形で表現されるグラフィカルな表現方法であり、強い相関関係にある変数同士を同じ色や形で表現することで、関係性をわかりやすく示すことができます。ヒートマップを用いることで、複数の変数間に存在する相関関係をよりわかりやすく捉えることができます。
相関分析のメリット
相関分析には、以下のようなメリットがあります。
・複数の変数間に存在する相関関係を捉えることができます。
・データの関係性をより深く理解することができます。
・予測や決定を支援することができます。
相関分析を用いることで、データ分析の上で大きな効果を挙げることができます。
相関分析のデメリット
相関分析には、以下のようなデメリットがあります。
・計算結果が誤っている可能性があります。
・多くの変数がある場合、分析が複雑になる可能性があります。
・相関関係が存在しない場合、誤った結論を導き出す可能性があります。相関分析を用いる際には、注意しておく必要があります。
相関分析の応用例
相関分析は、以下のような分野で応用されています。
・マーケティング:顧客の購入行動や嗜好を分析するために用います。
・金融:株価や為替の動向を分析するために用います。
・ 医療:病気の原因や治療効果を分析するために用います。相関分析は、様々な分野で役立つ分析手法です。
ヒートマップとは相関関係を示すものですか?
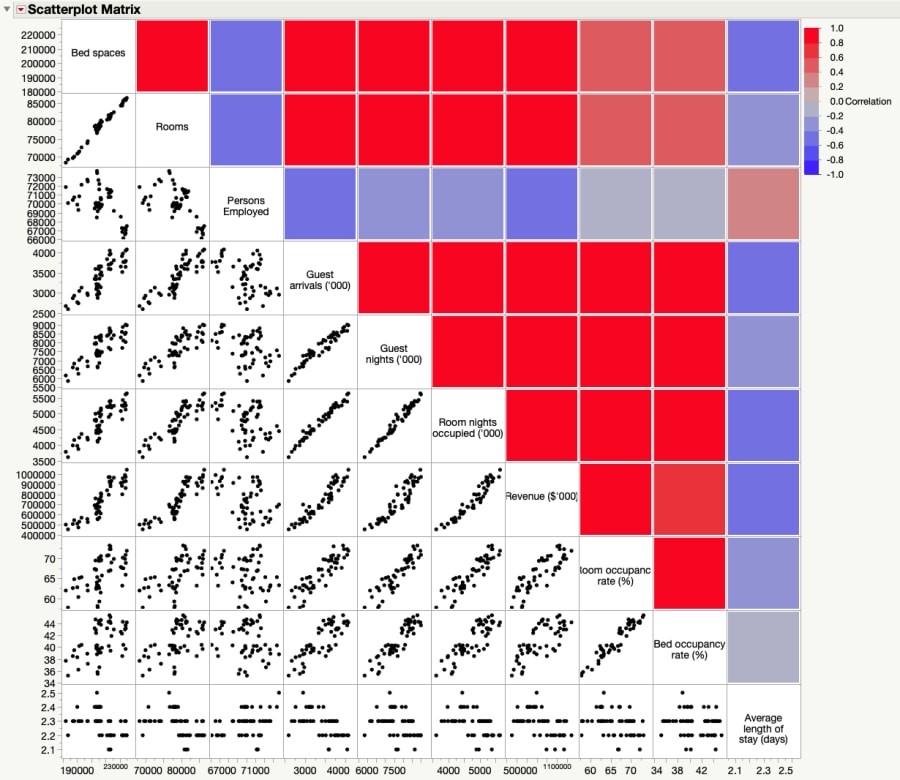
ヒートマップとは、データの視覚化技術の一つで、相関関係を示すものですが、それに限らない機能を持っています。相関関係を示すためには、ヒートマップを使用することで、複数の要因が相互に影響している関係を可視化することができます。
:h3 ヒートマップの特徴
ヒートマップは、データを色や大きさで表現することで、相関関係を示すことができます。特徴として、以下のような点が挙げられます。
- 簡潔な視覚化:ヒートマップは、複雑なデータを簡潔に視覚化することができます。
- 相関関係の可視化:ヒートマップは、相関関係を可視化することで、データの内在的な関係を明らかにすることができます。
- インタラクティブ:ヒートマップは、インタラクティブな機能を備えており、ユーザーがデータを詳細に調べることができます。
:h3 ヒートマップの適用範囲
ヒートマップは、様々な分野で適用することができます。特に、以下のような分野で有効です。
- マーケティング:ヒートマップは、マーケティングでの顧客分析や商品の売れ筋分析に使用することができます。
- 金融:ヒートマップは、株式や為替の分析に使用することができます。
- 医療:ヒートマップは、医療での疫学調査や疾患の特徴分析に使用することができます。
:h3 ヒートマップの作成方法
ヒートマップを作成するためには、以下のような手順を踏みます。
- データの収集:ヒートマップを作成するためのデータを収集します。
- データの前処理:収集したデータを前処理し、ヒートマップを作成する準備をします。
- ヒートマップの作成:前処理したデータを基にして、ヒートマップを作成します。
相関関係数とデータ数はどのように関係しますか?
相関関係数は、データ数に大きく影響されjejます。データ数が少ない場合、相関関係数は不正確になる可能性が高まります。特に、小さなデータセットでは、相関関係数はuropeanateになる可能性があります。
データ数が少ない場合の問題
データ数が少ない場合、相関関係数を計算する際には、以下のような問題が生じます。
Python3:Hit&Blowゲーム作成!コード解説付き- 標本のばらつきが大きくなり、サンプルバイアスが生じる。
- 相関関係数の計算結果が不確実になる。
- 検出力が低下し、誤検出の可能性が高まる。
大きなデータセットでの相関関係数
一方、大きなデータセットでは、相関関係数はより正確になります。以下のような利点があります。
- 標本のばらつきが小さくなり、サンプルバイアスが小さくなります。
- 相関関係数の計算結果がより確実になります。
- 検出力が高まり、誤検出の可能性が低まります。
データ数と相関関係数の関係のまとめ
以上の通り、データ数は相関関係数に大きく影響を及ぼします。特に、小さなデータセットでは注意を払う必要があります。以下は、データ数と相関関係数の関係をまとめたものです。
- 小さなデータセット:相関関係数が不正確になる可能性がある。
- 中程度のデータセット:相関関係数が比較的正確になる。
- 大きなデータセット:相関関係数がより正確になる。
相関行列からわかることは何ですか?
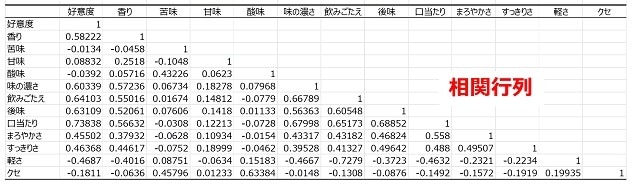
相関行列とは、統計学や機械学習において、複数の変数の相互関係を分析するために使用される行列です。この行列には、各変数間の相関係数が格納されており、相関係数が高ければ高いほど、両変数間に強い相関関係があることを示します。
相関行列の特徴
相関行列には、以下のような特徴があります。
Locust:負荷試験シナリオをhar2locustで自動生成!- 対称性:相関行列は対称行列であり、行と列を入れ替えても同じ値になります。
- 単位行列:相関行列の対角成分は1であり、自己相関係数を表します。
- 相関係数の範囲:相関係数は-1から1の範囲にあり、0に近いほど相関関係が弱くなります。
相関行列の用途
相関行列は、多くの分野で利用されています。
- 予測モデルの構築:相関行列を用いて、複数の変数間の相関関係を分析し、予測モデルの構築に役立つ情報を得ることができます。
- 特徴量選択:相関行列を用いて、相関関係が高い変数を選択し、特徴量として使用することができます。
- データの探索的分析:相関行列を用いて、データの相関関係を可視化し、データの特徴を把握することができます。
相関行列の注意点
相関行列を用いる場合には、以下のような注意点があります。
- 相関関係とは因果関係ではない:相関関係があるからといって、因果関係があるとは限りません。
- データの質:相関行列は、データの質に依存しており、データにノイズや偏りがあると、相関係数が誤る可能性があります。
- 多重共線性:相関行列では、多重共線性の問題が生じる可能性があり、相関係数が誤る可能性があります。
相関マップとは何ですか?

相関マップとは、何ですか?
相関マップは、複数の要素間に存在する相関関係を視覚的に表現するためのツールです。マップ上に相関する要素をプロットし、関係の強さや方向を示すことで、複雑な関係を把握することができます。相関マップは、社会科学、統計学、データサイエンスなどの分野で広く使用されています。
相関マップの特徴
相関マップの特徴として、以下のような点が挙げられます。
MirageSQL超入門:超初心者向けに解説!- 視覚的な表現:相関マップは、複数の要素間に存在する相関関係を視覚的に表現することができます。
- 関係の把握:マップ上に相関する要素をプロットし、関係の強さや方向を示すことで、複雑な関係を把握することができます。
- マルチディスクリプリン性:相関マップは、複数の変数間に存在する相関関係を捉えることができます。
相関マップの応用
相関マップは、以下のような分野で応用されています。
- 社会科学:相関マップは、社会調査や統計調査において、複数の要素間に存在する相関関係を把握するために使用されます。
- 統計学:相関マップは、統計分析において、変数間に存在する相関関係を捉えるために使用されます。
- データサイエンス:相関マップは、大量のデータを分析する際に、複数の要素間に存在する相関関係を把握するために使用されます。
相関マップの作成方法
相関マップを作成するためには、以下のような手順を踏みます。
- 相関係数の算出:相関係数を算出することで、要素間に存在する相関関係を把握することができます。
- マップの作成:相関係数を基にして、マップ上にプロットすることで、相関マップを作成することができます。
- マップの調整:作成されたマップを調整することで、よりわかりやすくすることができます。
よくある質問
相関分析とは何ですか?
相関分析は、統計学の手法の一つで、複数の変数の間に存在する相関関係を調べるための分析手法です。相関係数を計算することで、各変数の関係の強さや方向を把握することができます。この分析結果をもとに、データの内在的構造を捉えることができ、予測や意思決定のための有効な情報を導き出すことができます。
相関係数行列とは何ですか?
相関係数行列は、複数の変数の相関係数をまとめた表です。行列形式で表現されるため、視覚的に fácilmente 見やすく、複数の変数の関係を一望ですることができます。Heatmapと呼ばれる視覚化ツールを併用することで、相関係数の強さを可視化することができます。この相関係数行列を基にして、データのパターンや相関関係を把握することができます。
ヒートマップとは何ですか?
ヒートマップは、データの可視化ツールの一つで、色情報を用いてデータのパターンを表現します。相関係数行列と併用することで、相関係数の強さを可視化し、熱図のように表現することができます。視覚的にわかりやすく、データの内在的構造を捉えることができます。
相関分析の利点は何ですか?
相関分析の利点は、複数の変数の関係を把握できることです。予測精度を高めるために必要な情報を、わかりやすく抽出することができます。また、意思決定のための有効な情報を提供し、ビジネス上的な意思決定をサポートします。更に、データの内在的構造を捉えることで、データの理解を深めることができます。