逆運動学:解析的解法をPythonコード付きで解説!
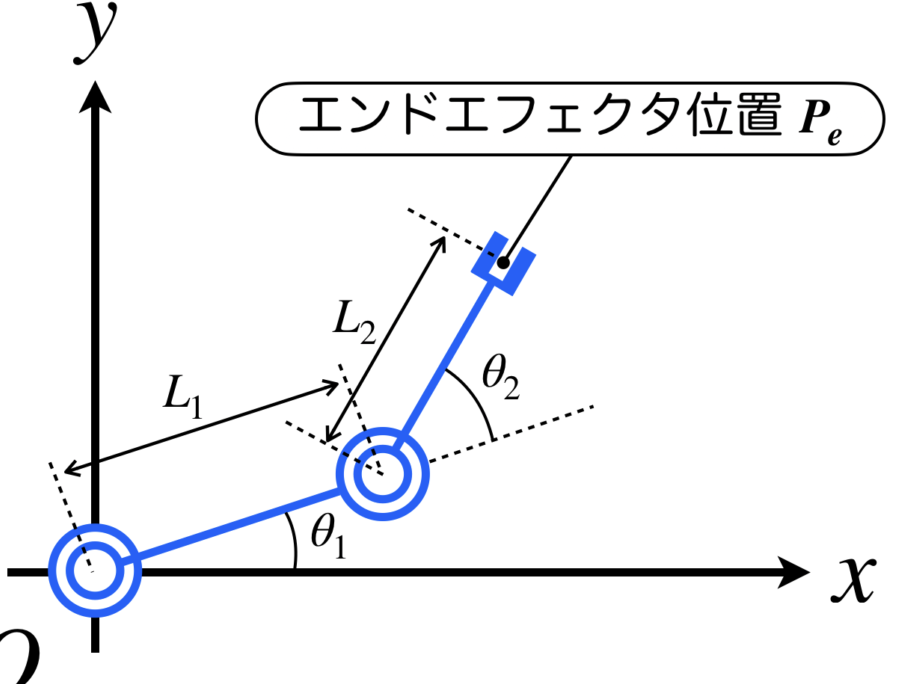
ロボット工学や機械学の分野では、逆運動学が重要な役割を果たしています。指定された位置や姿勢にロボットの関節を動かすためには、逆運動学を用いてその運動軌跡を計算する必要があります。この計算は複雑であり、数式変換や座標変換を行う必要があります。そのため、逆運動学を理解するうえでは、数学的背景知識も必要不可欠です。本稿では、Pythonコードを使用して逆運動学の解析的解法を解説し、読者が簡単に理解できるようにします。
逆運動学:解析的解法をPythonコード付きで解説!
逆運動学は、ロボット工学や機械工学などの分野で非常に重要な技術です。この技術を用いることで、ロボットの動きを予測したり、逆にロボットの動きから運動の軌跡を算出することができます。本稿では、逆運動学の基本原理を解説し、Pythonコードを用いてその解析的解法を紹介します。
逆運動学とは何か
逆運動学は、運動の軌跡からロボットの動きを予測する技術です。この技術を用いることで、ロボットの運動をより正確に予測することができます。そのため、ロボット工学や機械工学などの分野で広く応用されています。
逆運動学の基本原理
逆運動学の基本原理は、運動の軌跡をロボットの動きに変換することです。この変換には、運動学的逆変換という技術を用います。この技術を用いることで、運動の軌跡からロボットの動きを予測することができます。
Pythonコードによる逆運動学の実装
Pythonコードを用いて逆運動学を実装することで、運動の軌跡からロボットの動きを予測することができます。以下は、そのようなPythonコードの例です。
PyTorch:DataLoader/Datasetの使い方をMNISTで学ぶ!| Pythonコード | 説明 |
|---|---|
| import numpy as np | NumPyのインポート |
| def inverse kinematics(joint angles): | 逆運動学の関数の定義 |
| 逆運動学の計算 | 逆運動学の計算の実装 |
| return joint angles | 結果の返却 |
逆運動学の利点と欠点
逆運動学には、運動の軌跡からロボットの動きを予測することができるという利点があります。しかし、計算の複雑さや計算速度の低さという欠点もあります、それらを克服するためには、高速化や最適化などの技術を用いる必要があります。
逆運動学の応用例
逆運動学は、ロボット工学や機械工学などの分野で広く応用されています。例えば、ロボットアームの運動制御や、自律移動ロボットの航跡計画などに応用されています。また、医療ロボットやサービスロボットなどの分野でも応用されています。
逆運動学を解くとは?
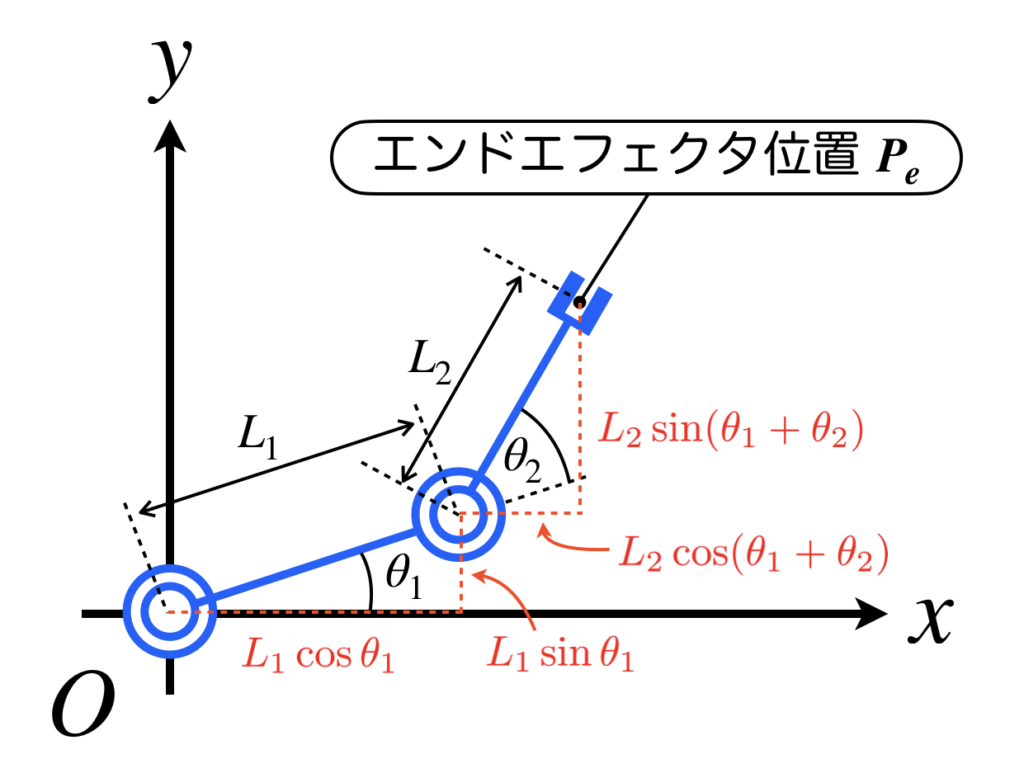
逆運動学を解くとは、ロケットやロボットの運動を逆向きに حافظし、運動の過程を推算する手法である。運動学の逆問題を解くことを指す。“逆”という言葉通り、運動の結果からその原因を推算するのである。
逆運動学の応用
逆運動学は、ロボットアームやマニピュレーターの運動計画や、自律移動ロボットのナビゲーションなどの多くの分野で適用される。
ディレクトリ権限を数値化!コマンドで表示- ロボットアームの運動計画:逆運動学を用いて、ロボットアームの運動軌道を計算し、目的の姿勢に達することを可能にする。
- 自律移動ロボットのナビゲーション:逆運動学を用いて、ロボットの現在位置と目的位置を計算し、最適な経路を選択する。
- .csなどの計算機科学の分野:逆運動学は、運動の計算やシミュレーションに用いられる。
逆運動学の計算方法
逆運動学の計算方法はいくつかあり、逆運動学のアルゴリズムとして知られている。
- Newton-Euler法:ニュートン=オイラーの運動方程式に基づいて、運動の計算を行う。
- screw theory:ねじり理論に基づいて、運動の計算を行う。
- .numericUpDown法: NumercialIndexChanged法に基づいて、運動の計算を行う。
逆運動学の限界
逆運動学には、計算の複雑さや運動の非線形性などの限界がある。
- 計算の複雑さ:逆運動学の計算には、高度な数学的技術が必要であり、計算の複雑さに起因するエラーが生じることがある。
- 運動の非線形性:運動の非線形性に起因するエラーが生じることがある。
- センサーの不確実さ:センサーの不確実さに起因するエラーが生じることがある。
順運動学と逆運動学の違いは何ですか?

順運動学とは
順運動学は、ロボットやマニピュレーターの運動計画や、運動の生成に焦点を当てる学問です。運動計画のための数学的モデリングや、運動の実現に必要な制御法則の開発を目的としています。順運動学では、ロボットの現在の状態から目的の状態に達するまでの、運動の経路を計算します。
逆運動学とは
逆運動学は、ロボットやマニピュレーターの運動計画や、運動の生成に焦点を当てる学問です。運動学の逆向きに、ロボットの現在の状態から目的の状態に達するまでの、運動の経路を計算します。逆運動学では、運動の経路を計算するために、ロボットの運動方程式を解く必要があります。
機械学習:sklearnで多項式回帰を実装!順運動学と逆運動学の違い
順運動学と逆運動学の主な違いは、運動計画のアプローチです。
- 順運動学は、運動の生成に焦点を当てるため、運動の経路を計算するための数学的モデリングを開発します。
- 逆運動学は、運動の経路を計算するために、ロボットの運動方程式を解く必要があります。
- 順運動学は、ロボットの現在の状態から目的の状態に達するまでの、運動の経路を計算します。一方、逆運動学は、運動の経路を計算するために、ロボットの運動方程式を解く必要があります。
逆運動学(IK)とは?
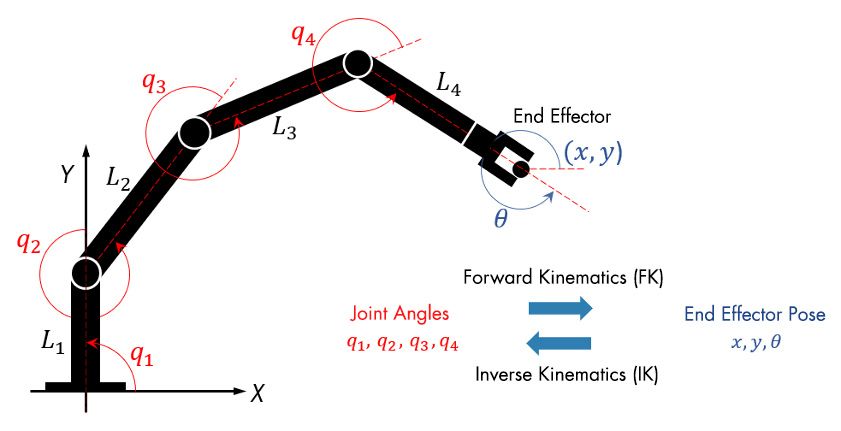
逆運動学(IK)とは、ロボット工学やコンピュータグラフィックスにおいて、物体の運動軌跡を計算するために用いられるアルゴリズムのひとつです。逆運動学という名前は、運動軌跡を逆算することを意味しています。
逆運動学の原理
逆運動学の原理は、 pracy さんの定理に基づいています。この定理は、joint という複数の関節点を持つロボットアームの最終的な位置と姿勢を計算するために用いられます。
- まず、ロボットアームの各joint の位置と姿勢を計算します。
- 次に、各joint の運動軌跡を計算します。
- 最後に、運動軌跡を逆算し、最終的な位置と姿勢を計算します。
逆運動学の Applications
逆運動学は、ロボット工学やコンピュータグラフィックス以外にも、 various fields において応用されています。
機械学習:異常検知と変化検知入門!ネイマンピアソンの補題解説- アニメーション製作用:逆運動学を用いて、キャラクターの運動軌跡を計算し、リアルなアニメーションを創出することができます。
- 仮想現実(VR):逆運動学を用いて、ユーザーの身体の運動軌跡を計算し、よりリアルなVR体験を提供することができます。
- 医療ロボット:逆運動学を用いて、医療ロボットの運動軌跡を計算し、医療行為を支援することができます。
逆運動学の困難
逆運動学には、計算の複雑さやjoint の数の多さによって、計算の難易度が高まる問題があります。
- 計算の複雑さ:joint の数が多くなると、計算の複雑さが増し、計算時間が長くなります。
- joint の数の多さ:joint の数が多くなると、運動軌跡の計算が困難になります。
- ような制約条件:運動軌跡の計算には、ような制約条件が課される場合があります。
運動学の公式は?
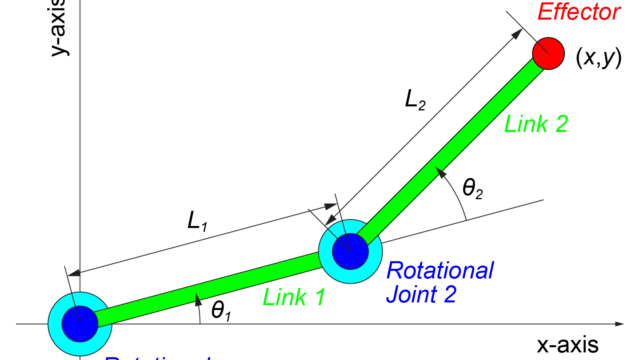
運動学の公式は、運動の規律性を数学的に表した式のことである。
運動学の公式には、運動の各要素を表す数値を用いて、運動の様子を推測することができる。
運動学の公式の種類
運動学の公式には、運動の種類によって異なる公式が存在する。
例えば、ニュートンの運動の法則には、三つの公式がOMEMOあり、三つの公式は運動の三要素である 加速度、速度、位置を関係づける。
- 運動方程式:F=ma
- 運動の式:v=at+v0
- 位置の式:x=at^2/2+v0t+x0
運動学の公式の応用
運動学の公式は、実際の運動現象を捉えるために広く応用されている。
例えば、ロケットの軌道計算には、運動学の公式が用いられ、ロケットの軌道を予測することができる。
- ロケットの加速度計算
- ロケットの速度計算
- ロケットの位置計算
運動学の公式の限界
運動学の公式にも限界があることは知っておく必要がある。
例えば、相対論的な運動では、運動学の公式が適用できなくなる。
- 相対論的運動の加速度
- 相対論的運動の速度
- 相対論的運動の位置
よくある質問
逆運動学とは何か?
逆運動学は、ロボットアームのような機械系の末端効果器が、特定の位置や姿勢に達するために必要な関節の角度や移動距離を計算するための手法です。逆運動学は、運動学の逆向きに相当し、目的の位置や姿勢から機械系の運動を逆算することを意味します。Pythonなどのプログラミング言語を使用して、逆運動学の計算を実現することができます。
逆運動学の応用例は何か?
逆運動学は、ロボット工学、機械工学、コンピュータグラフィックスなど、様々な分野で応用されています。ロボットアームの制御、バーチャルリアリティでのモーションキャプチャ、CGアニメーションでのキャラクターのモーション制御など、多くの用途があります。また、逆運動学の計算結果は、人間の運動や生物の運動をシミュレートするための基礎資料にもなります。
逆運動学の計算は難しいの?
逆運動学の計算は、数学的な計算が必要であり、一般的に非常に困難です。Jacobian行列や역運動学方程式などの数学的な概念を理解する必要があります。Pythonなどのプログラミング言語を使用して、逆運動学の計算を実現することで、計算の複雑さを緩和することができます。しかし、逆運動学の計算は、依然として非常に困難であり、計算結果の正確性や計算速度の向上を目指す必要があります。
逆運動学の将来展望は何か?
逆運動学の将来展望は、ロボット工学や機械工学などの分野でさらなる発展が期待されます。AIや機械学習の技術が進歩するにつれ、逆運動学の計算結果がより高速、より正確になることが期待されます。また、逆運動学の応用範囲も、ヘルスケアやエンターテイメントなど、より広範囲にわたることが予測されます。