2の補数:負数表現の仕組みを解説!

コンピューターが負の数を扱う際には、2の補数という特殊な表現方法を用いることが多い。この方法では、通常の十進数字ではなく、二進数字に基づいて負の数を表現することになる。这样的表現方法には、プログラマーやエンジニアにとっては必須の知識だが、とは言え一般的にはあまり知られていない ‘{@2の補数}’ について、ここではその仕組みや原理を詳しく解説していく。

2の補数:負数表現の仕組みを解説!
2の補数は、コンピューターの内部で負数を表現するための方法の一つです。この方法では、正数と負数を同様の形式で表現することができます。
2の補数の原理
2の補数は、ビット列を反転して1を加えることで、負数を表現することができます。この方法は、加算や乗算などの演算を行うときに便利です。反転と加算の2つのステップで負数を表現することができます。
2の補数の表現形式
2の補数では、正数と負数を同様の形式で表現することができます。例えば、8ビットの2の補数では、00000001は1を、10000001は-1を表現します。ビットパターンが異なるだけで、内容は同じです。
2の補数の利点
2の補数には、以下のような利点があります。簡単な演算、高速な計算、メモリーの削減などです。特に、計算機内部での負数の表現には非常に有効です。
ELT:ETLに代わるデータ統合手法!なぜ流行っているのか?2の補数の応用
2の補数は、コンピューターの内部だけでなく、デジタル信号処理や insanın認識などの分野でも応用されています。画像処理や音声処理でも、2の補数を使用することで高速で正確な処理を行うことができます。
2の補数の注意点
2の補数には、注意点もあります。オーバーフローやアンダーフローなど、計算結果が異なる場合があります。したがって、2の補数を使用するときには注意しておく必要があります。
| 表現形式 | 値 |
|---|---|
| 00000001 | 1 |
| 10000001 | -1 |
| 11111110 | -2 |
| 01111111 | 127 |
負数を2の補数で表す理由は?

負数を2の補数で表す理由は、コンピュータの内部的な表現方法に根ざしている。コンピュータでは、二進法(バイナリ)を使用して情報を扱うため、負数を表すために2の補数を使用する。
コンピューターの数値表現
コンピューターの内部では、ビット(bit)という単位で情報を扱う。ビットは0か1の2つの値を持つため、二進法を使用して数値を表現する。コンピューターでは、整数を符号付き整数(signed integer)や符号なしか整数(unsigned integer)として扱う。
Splunk CLI:よく使うコマンドまとめ!2の補数の利点
2の補数を使用することで、計算の簡略化や高速化が可能になる。
- 加算や減算の計算が簡単になる。
- 補数を使用することで、桁上げや桁借りを省くことができる。
- 2の補数を使用することで、計算の結果が小さくなるため、メモリーの容量を節約できる。
符号付き整数と2の補数
符号付き整数は、最上位ビットを符号ビットとして使用して、負数を表現する。
- 符号ビットが0の場合は正数、1の場合は負数を表す。
- 2の補数を使用することで、負数を正数の形に変換することができる。
- 符号付き整数には、オーバーフロー(overflow)やアンダーフロー(underflow)という問題があるが、2の補数を使用することで、これらの問題を解消できる。
負の数を2の補数で表現するには?

負の数を2の補数で表現するには、以下のような方法で表現することができます。
2の補数表現の原理
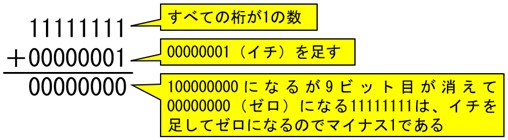
2の補数表現では、ビット長を決めておき、負の数をそのビット長に合わせて表現する。最上位ビットが1の場合は負の数、0の場合は正の数を表すことになる。例えば、8ビットの2の補数表現では、-1を11111111、-2を11111110、-3を11111101、…と表現することができます。
数学TeX記法まとめ:数式を美しく記述!2の補数表現の計算方法
2の補数表現を行うには、まずその数を10進数で表現し、ビット長に合わせて2進数に変換する。反転を行い、その結果に1を加えることで2の補数表現を計算することができます。例えば、-5を8ビットの2の補数表現に変換するには、まず10進数の-5を2進数に変換し、101を得る。次に反転を行い、010に変換する。最後に1を加え、011に変換することで、-5を2の補数表現に変換することができます。
2の補数表現の利点
2の補数表現には、以下のような利点があります。
- 負の数を簡単に表現することができます。
- 加減算の計算が簡単になります。
- ハード웨어での処理が容易になります。
2の補数表現とはどういう意味ですか?
2の補数表現とは、符号付き2の補数を用いて数値を表現する方式のことを指します。この方式では、負の数値を表現するために符号ビットを使用し、数値の絶対値を符号付き2の補数に変換します。
符号付き2の補数の特徴
2の補数表現には、以下のような特徴があります。
アナログ出力解説:電子回路の基本!- 符号ビットを使用して負の数値を表現することができます。
- オーバーフローを検出することができます。
- 符号付き2の補数に変換することで、演算の高速化を実現できます。
2の補数表現の計算方法
2の補数表現を行うためには、以下のような計算方法を用います。
- 数値の絶対値を計算します。
- 符号ビットを計算します。
- 符号ビットと絶対値を組み合わせて、符号付き2の補数を生成します。
2の補数表現の応用例
2の補数表現は、コンピューターの内部表現や、デジタル信号処理など、様々な分野で応用されています。
- コンピューター内部での数値表現
- デジタル信号処理における数値計算
- 暗号化や圧縮技術での数値表現
2の補数の作り方は?
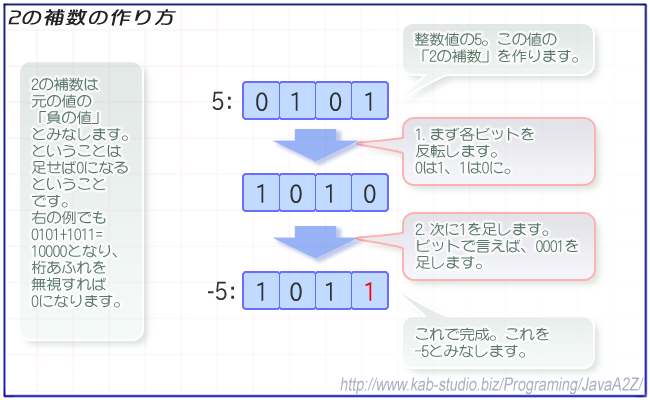
2の補数の作り方は、 principlamente、減算を行うことで実現されます。減算とは、ある数から他の数を引くことです。例えば、2の補数を作りたい場合、2を引く数を探します。2の補数を作るには、2のバイナリ表現にマスクを適用する必要があります。
2の補数の作り方の例
例えば、2進数での数値1101(十進数では13)について、2の補数を作りたい場合、まずバイナリ表現を取得します。1101を反転させたものは、0010となります。これを反転させた数値に1を加えると、0011になります。这就是2の補数です。
Android:ボタンにマテリアルデザインアイコンを追加!2の補数の性質
2の補数には、以下のような性質があります。
- 2の補数を作るには、バイナリ表現にマスクを適用する必要があります。
- 2の補数は、減算を行うことで実現されます。
- 2の補数は、反転させた数値に1を加えることで実現されます。
2の補数の应用
2の補数は、コンピューターの計算において広く利用されています。例えば、符号つき整数の表現や位操作において、2の補数が使用されます。
- 符号つき整数の表現:2の補数を使用することで、符号つき整数を簡単に表現することができます。
- 位操作:2の補数を使用することで、ビットの反転やシフトを行うことができます。
- 計算の高速化:2の補数を使用することで、計算の高速化が期待できます。
よくある質問
2の補数とは何ですか?
2の補数は、二進数を用いて負の数を表現するための方法です。通常の二進数では、負の数を表現することができませんが、2の補数を用いることで負の数を表現することができます。2の補数では、ビット反転を行い、さらに 1 を加える ことで負の数を表現します。この方法を用いることで、計算機内部での負の数の表現や計算を効率的に行うことができます。
2の補数の仕組みはどのように動作しますか?
2の補数の仕組みは、ビット反転と 1 の加算 の2つのステップで構成されています。まず、負の数を表現したい 二進数 を取得し、各ビットを反転させます。次に、反転されたビット列に 1 を加える ことで、負の数を表現した二進数を生成します。この二進数を用いることで、計算機内部での負の数の計算を効率的に行うことができます。
2の補数の利点は何ですか?
2の補数の利点は、負の数の表現 と 計算の効率化 の2点にあります。通常の二進数では、負の数を表現することができませんが、2の補数を用いることで負の数を表現することができます。また、2の補数を用いることで、計算機内部での負の数の計算を効率的に行うことができます。このため、計算機の性能を向上させることができます。
2の補数はどこで使われているのですか?
2の補数は、コンピューター や 携帯電話 などの電子機器での数値計算に広く使われています。特に、マイプロセッサー や 中央処理装置 などの計算機内部での数値計算に際しては、2の補数が広く使われています。また、プログラミング や ソフトウェア開発 などの分野でも、2の補数の知識が必要不可欠です。